- El mes de junio de 2015, el primer tema tratado correspondió a Vector Gradiente y Derivada Direccional:
BIBLIOGRAFÍA:
http://vidaenelespiritu.com/cvv/4.5_vector_gradiente_y_derivada_direccional.pdf
2.- El segundo tema tratado en el curso durante el mes de junio correspondió a Diferenciales e Incrementos Diferenciales:
Diferenciales e incrementos diferenciales:
Para funciones de una variable  , se define el incremento de
, se define el incremento de  como
como
y la diferencial de  como
como
En la siguiente figura se muestra  .
.
Figura 1: diferencial
Observe que  se aproxima a cero más rápidamente que
se aproxima a cero más rápidamente que  , ya que
, ya que
y al hacer  , tenemos que
, tenemos que  .
.
Por tanto
donde  conforme
conforme  .
.
Ahora consideremos una función de dos variables
Si  y
y  son incrementados
son incrementados  y
y  , entonces el correspondiente incremento de
, entonces el correspondiente incremento de  es
es
Con lo cual  representa el cambio en el valor de
representa el cambio en el valor de  cuando
cuando  cambia a
cambia a  .
.
| Definición | |
| Sean |
BIBLIOGRAFÍA:
- http://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/SUPERIOR/t5-Incrementos-diferenciales/node1.html
3.- El tercer tema tratado en el curso de
Cálculo Vectorial en el mes de junio
correspondió a Planos Tangentes a una Superficie y Recta Tangente:



4.- El cuarto tema tratado en el curso de Cálculo Vectorial correspondió a Máximos y Mínimos:

Cálculo Vectorial en el mes de junio
correspondió a Planos Tangentes a una Superficie y Recta Tangente:



4.- El cuarto tema tratado en el curso de Cálculo Vectorial correspondió a Máximos y Mínimos:
Máximos y mínimos:
Una función z=f(x,y) tiene un máximo relativo (MR) en (a,b)
- Si: f(x,y)≤ f(a,b), cuando (x,y) está cerca de (a,b). El valor (a,b) recibe el nombre de máximo relativo de f(x,y).
- Si f(x,y)≥ f(a,b), cuando (x,y) está cerca de (a,b), entonces se dice que f(x,y) tiene un mínimo relativo (mR) en (a,b).
NOTA: Un punto de silla son puntos donde la f(x,y) presenta un MR con respecto a la una variable y un mR con respecto a la otra, a la vez.
Criterio de la segunda derivada:
El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
Sea  una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
- Si
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. - Si
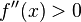 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Si  , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
Hallar las derivadas parciales de f con respecto a x y a y.
Igualar a cero las derivadas parciales encontradas anteriormente y encontrar los puntos críticos.
Hallar las derivadas parciales de segundo orden Fxx; Fxy; Fyy.
Determinar cada segunda derivada en los puntos críticos.
Cálculo de máximos y mínimos:
1. Hallamos la derivada primera y calculamos sus raíces.
2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella las raíces de derivada primera y si:
f''(a) < 0 es un máximo relativo
f''(a) > 0 es un mínimo relativo
3. Calculamos la imagen (en la función) de los extremos relativos.
Ejemplo
f(x) = x3 − 3x + 2
f'(x) = 3x2 − 3 = 0
f''(x) = 6x
f''(−1) = −6 Máximo
f''(1) = 6 Mínimo
f(−1) = (−1)3 − 3(−1) + 2 = 4
f(1) = (1)3 − 3(1) + 2 = 0
Máximo(−1, 4) Mínimo(1, 0)
Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:
1. Un máximo en el punto, de la función, en la que ésta pasa de creciente a decreciente.
2. Un mínimo en el punto, de la función, en la que ésta pasa de decreciente a creciente.
Ejemplo
Hallar los máximos y mínimos de:
Tenemos un mínimo en x = 3
 Mínimo(3, 27/4)
Mínimo(3, 27/4)
En x = 1 no hay un máximo porque x = 1 no pertenece al dominio de la función.
MÁXIMOS Y MÍNIMOS CONDICIONADOS:
Multiplicadores de Lagrange.
En los problemas de optimización, el método de los multiplicadores de Lagrange, llamados así en honor a Joseph Louis Lagrange, es un procedimiento para encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones. Este método reduce el problema restringido con n variables a uno sin restricciones de n + k variables, donde k es igual al número de restricciones, y cuyas ecuaciones pueden ser resueltas más fácilmente. Estas nuevas variables escalares desconocidas, una para cada restricción, son llamadas multiplicadores de Lagrange.
El método dice que los puntos donde la función tiene un extremo condicionado con k restricciones, están entre los puntos estacionarios de una nueva función sin restricciones construida como una combinación lineal de la función y las funciones implicadas en las restricciones, cuyos coeficientes son los multiplicadores.
Máximos y mínimos condicionados:
Se llama un extremo condicionado de una función f(x,y) al máximo o mínimo de esta función alcanzado con la condición de que sus variables independientes enten relacionadas entre sí mediante la ecuación:
g(x,y)=o (Ecuación de enlace)
Para hallar los extremos condicionados se forma la llamada FUNCIÓN DE LAGRANGE.

Donde gama es una constante llamada: Multiplicador de Lagrange
Luego se determinan los Máximos relativos de la función de Lagrange.
Matematicamente se siguio probando el postulado y se llego a la conclución de que:

Matematicamente se siguio probando el postulado y se llego a la conclución de que:

Los extremos de la función f(x,y) condicionados por la restricción g(x,y)=0, se producen en los puntos críticos de la función de Lagrange:
Condiciones necesarias de extremo.
Las condiciones necesarias del extremo de una función de Lagrange vienen dadas por el sistema de ecuaciones.
Para resolver el sistema, eliminamos  de las dos primeras ecuaciones y el resultado lo sustituimos en la tercera (procurando no perder soluciones con las simplificaciones).
de las dos primeras ecuaciones y el resultado lo sustituimos en la tercera (procurando no perder soluciones con las simplificaciones).
Condiciones suficientes para la existencia de extremos.
(a) Caso de dos variables.
Sea  un punto crítico de la función de Lagrange
un punto crítico de la función de Lagrange  , obtenido para un valor concreto
, obtenido para un valor concreto  . Formamos la función de Lagrange para ese
. Formamos la función de Lagrange para ese 
Para estudiar su naturaleza podemos seguir dos caminos:
(a-1) Método de la diferencial segunda:
El problema de la existencia y el carácter del extremo condicional se resuelve averiguando el signo de la segunda diferencial de la función de Lagrange (particularizada para  )
)
a condición de que: 
Si  la función tiene un mínimo condicionado, y si
la función tiene un mínimo condicionado, y si  la función tiene un máximo condicionado.
la función tiene un máximo condicionado.
BIBLIOGRAFÍA:
- http://www.dtic.upf.edu/~gharo/anum/apunts/hessian.pdf
- http://fernandorevilla.es/maximos-y-minimos-condicionados-multiplicadores-de-lagrange/
- http://claroline.emate.ucr.ac.cr/claroline/claroline/backends/download.php?url=L0V4dHJlbW9zX0Z1bmNpb25lc19WYXJpYXNfVmFyaWFibGVzLnBkZg%3D%3D&cidReset=true&cidReq=0MA1023
- https://sites.google.com/site/proyectoformativodematematica/3-contenidos/14-optimizacion-con-restriccion-matriz-hessiana-multiplicadores-de-lagrange
5.- El quinto tema estudiado en el curso de Cálculo Vectorial en el mes de junio correspondió a:
Integrales sobre Regiones Rectangulares:


Integrales sobre Regiones Generales:






APLICACIONES DE LAS INTEGRALES DOBLES




INTEGRALES TRIPLES



APLICACIONES DE LAS INTEGRALES TRIPLES




CAMBIOS DE COORDENADAS A CILÍNDRICAS Y ESFÉRICAS CON JACOBIANO



BIBLIOGRAFÍA:


Campo Vectorial en R 3:


7.- El último tema estudiado en el curso de Cálculo Vectorial en el mes de junio correspondió a:



Parametrización:



Integrales sobre Regiones Rectangulares:


Integrales sobre Regiones Generales:


INTEGRALES DOBLES

La integral doble se define como sigue:


EJEMPLO:

APLICACIONES DE LAS INTEGRALES DOBLES




INTEGRALES TRIPLES



APLICACIONES DE LAS INTEGRALES TRIPLES




CAMBIOS DE COORDENADAS A CILÍNDRICAS Y ESFÉRICAS CON JACOBIANO


EJEMPLO:
BIBLIOGRAFÍA:
- ocw.upc.edu/download.php?file=15012553/34717-3401.pdf
- https://es.wikipedia.org/wiki/Integral_múltiple
- https://www.uam.es/personal_pdi/ciencias/fchamizo/.../resumen02.pdf
6.- El sexto tema estudiado en el curso de Cálculo Vectorial en el mes de junio correspondió a:
CAMPOS VECTORIALES
- Campo Vectorial en R 2:




7.- El último tema estudiado en el curso de Cálculo Vectorial en el mes de junio correspondió a:
DEFINICIÓN DE INTEGRAL DE LÍNEA:




Parametrización:

EJEMPLO:
BIBLIOGRAFÍA:
- https://docs.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/edit
- www.ehu.eus/~mtpalezp/libros/06_4.pdf













No hay comentarios.:
Publicar un comentario